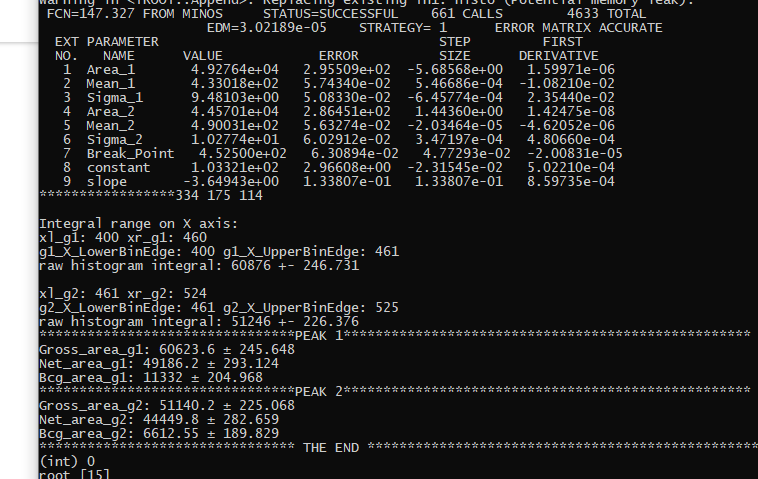
I forgot. Is this epsilon (1e-6) related to the precision of finding the mean? Should I keep playing with that number until the roundoff error is demolished? I found Moneta mentioned about that.
My conclusion: error disappears as I play with my integral limits. If I go from Lower bin 400 to upper bin 530, I see NO ERROR. Thus, it’s a matter of limits and the ability of fitting procedure within those limits. Am I right?
I see the terminal resuls and the fit result DONOT MATCH. First parameters of each gaussian should be the integral of those peaks due to the usage of Gausn, but the results give different outcomes comparison to parameter outcomes.
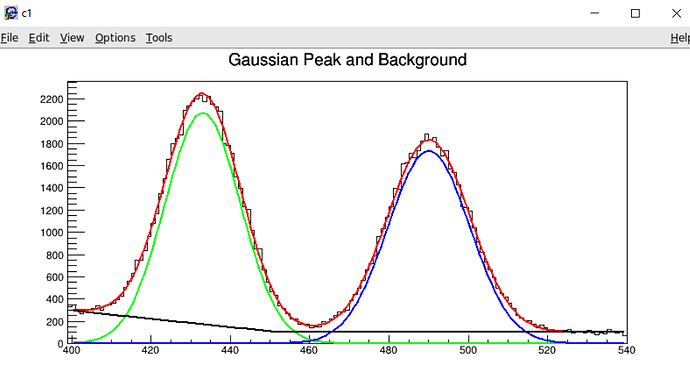
One more thing is that the broken line is not broken where I set the value. I want it to break at the bin number 462. Why is that?
What about my 3rd question?